Entropy Analysis to Understand LLM Hallucinations

This article shows how we can leverage entropy to detect LLM hallucinations efficiently.

The concept of entropy spans multiple fields of study. It first emerged in thermodynamics to measure how many different states are possible in a system, essentially quantifying its level of randomness. This foundational idea was later adapted by Claude Shannon for information theory, giving birth to what we now call "Shannon entropy."

$H(X) = -\sum_{i=1}^n P(x_i)\log_2P(x_i)$

The entropy H(X) measures uncertainty in a system X that has n different possible outcomes, with each outcome having its own probability P(xi).

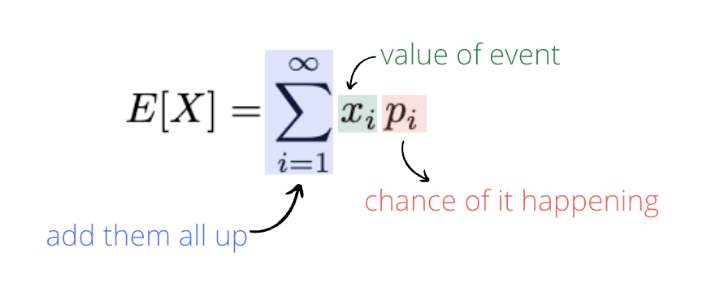
LLMs generate text by selecting tokens sequentially. For each selection, the model calculates probabilities for potential next tokens and typically chooses the most probable one (though this can be adjusted through steering settings). If you have access to these probability distributions the model generates, you can calculate the entropy at each token selection step.

But looking at entropy calculations alone won't reveal if an LLM truly understands what it's saying. This limitation exists because human language offers multiple valid ways to express the same idea. For example, there could have been many equally appropriate responses to this question:

Simply calculating entropy from the raw probabilities is not enough, since there are many ways to say the same thing. But when we group answers by their actual meaning (clustering+embeddings), we get a clearer picture. Their semantic entropy method better indicates when an LLM is providing factual answers versus making things up.

Let's consider the example "Describe the weather: It is"

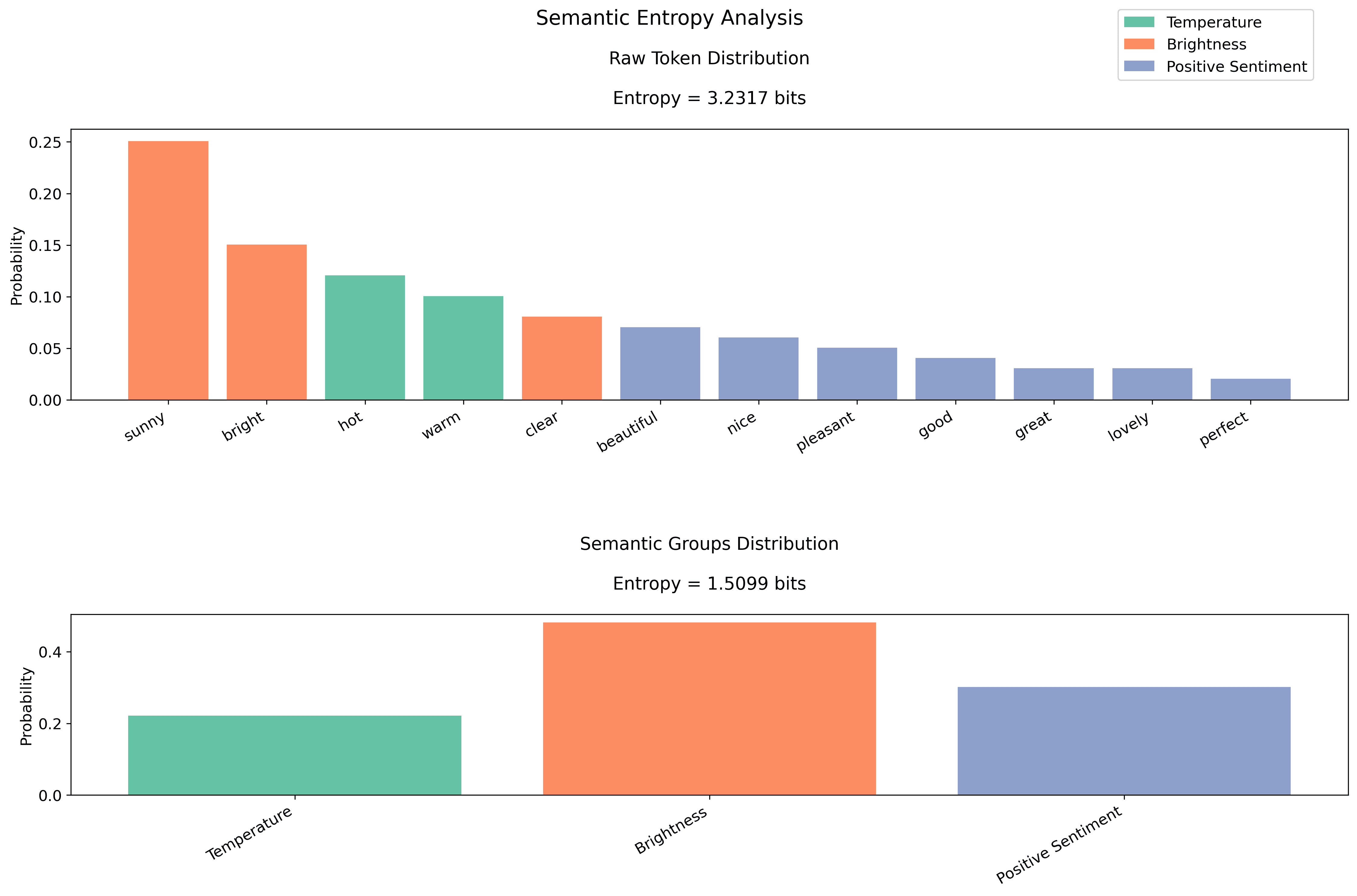
Semantic entropy:
$H_s = -\sum_{j=1}^m P(g_j) \log_2P(g_j)$

• Where g_j represents semantic groups

Practical Interpretation:

• If entropy = 1 bit: model is choosing between 2 equally likely options

• If entropy = 2 bits: model is choosing between 4 equally likely options

• If entropy = 3 bits: model is choosing between 8 equally likely options

• Our semantic entropy reduction (from 3.1 to 1.5 bits) shows we've reduced complexity from ~8 choices to ~3 effective choices

This is great and bring structure to our evaluation algorithm. But we are still not completely satisfied.. how we can measure the surprise factor?

Semantic entropy helps us understand how many different ideas a model is considering, but it doesn't tell us about the model's relative confidence in those different options. This is where varentropy comes in. Varentropy measures how much the model's confidence varies across different token predictions.

It is calculated as the variance of the information content (surprisal) across token probabilities:

$V(X) = \sum_{i=1}^n P(x_i)(-\log_2P(x_i) - H(X))^2$

Where

• P(x_i) is the probability of token i

• H(X) is the entropy (average information content)

• n is the number of tokens being considered

To make it more clear:

So, now let's start the experiment and see how far we can go considering semantic entropy and varentropy.

Experimental Setup

We did a comprehensive analysis to see how language models handle different types of content through the lens of semantic entropy and varentropy. Our experiment utilized the Qwen2.5 0.5B base model (TGI) engine for inference.

Dataset Composition:

• Sample size: N=2k prompts

• Minimum token length: 20 tokens per prompt

• Five distinct categories:

  1. Factual statements (e.g., scientific facts, historical events)

  2. Hallucinations (intentionally nonsensical or impossible scenarios)

  3. Subjective opinions (personal preferences, judgments)

  4. Ambiguous statements (multiple valid interpretations)

  5. Edge cases

We designed our experiment to examine the model's thought process by analyzing its token probability distributions when completing partial phrases. Each prompt was carefully semi-manually crafted.

The hypothesis is that hallucinations would display distinctly different entropy signatures compared to factual or ambiguous statements.

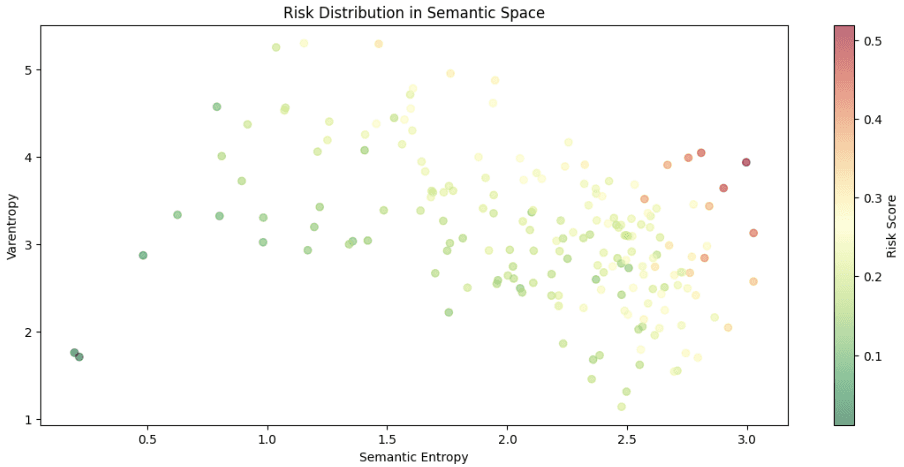
The scatter plot of semantic entropy vs. varentropy reveals a clear pattern: - Low semantic entropy (0.5-1.5) correlates with factual statements - Higher semantic entropy (2.0-3.0) typically indicates hallucinations - As semantic entropy increases, we see higher varentropy, suggesting increased model uncertainty - The color gradient shows a clear progression from low-risk (green) to high-risk (red) predictions

Key Insights

1. The combination of semantic entropy and varentropy proves to be a powerful tool for detecting hallucinations. When a model starts "making things up," both metrics increase significantly.

2. The clear separation in semantic space suggests we can reliably identify when a model is operating in factual versus hallucinatory modes.

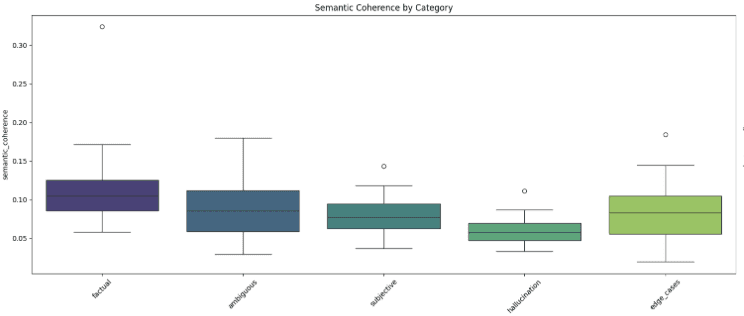
3. Edge cases reveal the nuanced nature of AI reasoning - they often sit between factual and hallucinatory territories, much like human uncertainty in frontier scientific theories or philosophical questions.

This findings have several useful applications:

• Quality control for AI-generated content

• Real-time hallucination detection in AI systems

• Confidence scoring for AI outputs

• Better understanding of model uncertainty

While promising, this approach has some limitations: binary tendencies & challenges with highly contextual statements.

Semantic entropy and varentropy provide an analytical way for understanding and detecting AI hallucinations. By measuring both the diversity of potential responses (semantic entropy) and the model's uncertainty in those responses (varentropy), we can effectively identify when an AI system is operating beyond its knowledge boundaries.

Our reward models leverage these concepts enabling the reduction of uncertainty and hallucinations by 5-7x in production.

Can we teach LLMs to ask for human help when they reach their reasoning limits? Would AI self-reflection provide the same type of risk classification?

Stay tuned for more updates!